lunes, 1 de abril de 2013

Ley de Hooke

Originalmente formulada para casos del estiramiento longitudinal, establece que el alargamiento unitario que experimenta un material elástico es directamente proporcional a la fuerza aplicada :

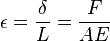
\epsilon = \frac{\delta}{L} = \frac{F}{AE}

  • Alargamiento:
                \delta
  • Longitud Original:
               L
  • Modulo de Young:
               E
  • Sección transversal de la pieza estirada:
               A

  1. La ley se aplica a materiales elásticos hasta un límite denominado límite elástico.
  2. La ley de Hooke describe cuanto se alargará un resorte bajo una cierta fuerza.







  • Ley de Hooke para los resortes:
La forma más común de representar matemáticamente la Ley de Hooke es mediante la ecuación del muelle o resorte, donde se relaciona la fuerza  ejercida sobre el resorte con la elongación o alargamiento  producido:
F = - k\delta \,


  • Ley de Hooke en sólidos elásticos:
En la mecánica de sólidos deformables elásticos la distribución de tensiones es mucho más complicada que en un resorte o una barra estirada sólo según su eje. La deformación en el caso más general necesita ser descrita mediante un tensor de deformaciones mientras que los esfuerzos internos en el material necesitan ser representados por un tensor de tensiones. Estos dos tensores están relacionados por ecuaciones lineales conocidas por ecuaciones de Hooke generalizadas o ecuaciones de Lamé-Hooke, que son las ecuaciones constitutivas que caracterizan el comportamiento de un sólido elástico lineal. Estas ecuaciones tienen la forma general:

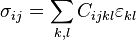
\sigma_{ij} = \sum_{k, l} C_{ijkl}\varepsilon_{kl} \,

Gran parte de las estructuras de ingeniería son diseñadas para sufrir deformaciones pequeñas,se involucran sólo en la recta del diagrama de esfuerzo y deformación.
De tal forma que la deformación  es una cantidad a dimensional  el modulo  se expresa en las mismas unidades que el esfuerzo  (unidades pa, psi y ksi). El máximo valor del esfuerzo para el que puede emplearse la ley de Hooke en un material es conocido como límite de proporcionalidad de un material. En este caso, los materiales dúctiles que poseen un punto de decencia definido; en ciertos materiales no puede definirse la proporcionalidad de decencia fácilmente, ya que es difícil determinar con precisión el valor del esfuerzo  para el que la similitud entre  y  deje de ser lineal. Al utilizar la ley de Hooke en valores mayores que el límite de proporcionalidad no conducirá a ningún error significativo. En resistencia de materiales se involucra en las propiedades físicas de materiales, como resistencia, ductilidad y resistencia de corrosión; que pueden afectarse debido a la aleación, el tratamiento térmico y el proceso de manofactura.

  • Caso unidimensional:
En el caso de un problema unidimensional donde las deformaciones o tensiones en direcciones perpendiculares a una dirección dada son irrelevantes o se pueden ignorar , ,  y la ecuación anterior se reduce a:

\sigma = E\epsilon \,

donde E es el módulo de Young.

  • Caso tridimensional isótropo:
Para caracterizar el comportamiento de un sólido elástico lineal e isótropo se requieren además del módulo de Young otra constante elástica, llamada coeficiente de Poisson (). Por otro lado, las ecuaciones de Lamé-Hooke para un sólido elástico lineal e isótropo pueden ser deducidas del teorema de Rivlin-Ericksen, que pueden escribirse en la forma:


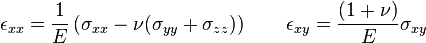
\epsilon_{xx} = \frac{1}{E}\left( \sigma_{xx} - \nu(\sigma_{yy}+\sigma_{zz}) \right) \qquad \epsilon_{xy} = \frac{(1+\nu)}{E}\sigma_{xy}
Formulas De Caso Tridimensional Isotropo

  • Caso tridimensional ortótropo:

    El comportamiento elástico de un material orto trópico queda caracterizado por nueve constantes independientes: 3 módulos de elasticidad longitudinal , 3 módulos de rigidez  y 3 coeficientes de Poisson . De hecho para un material orto trópico la relación entre las componentes del tensor tensión y las componentes del tensor deformación viene dada por:
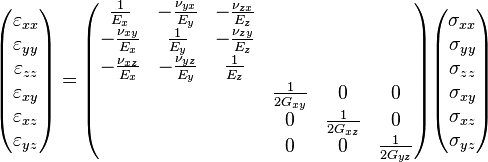
\begin{pmatrix} \varepsilon_{xx}\\ \varepsilon_{yy}\\ \varepsilon_{zz}\\ \varepsilon_{xy}\\ \varepsilon_{xz}\\ \varepsilon_{yz} \end{pmatrix} = \begin{pmatrix} \frac{1}{E_x} & -\frac{\nu_{yx}}{E_y} & -\frac{\nu_{zx}}{E_z} & & & \\ -\frac{\nu_{xy}}{E_x} & \frac{1}{E_y} & -\frac{\nu_{zy}}{E_z} & & & \\ -\frac{\nu_{xz}}{E_x} & -\frac{\nu_{yz}}{E_y} & \frac{1}{E_z} \\ & & & \frac{1}{2G_{xy}} & 0 & 0 \\ & & & 0 & \frac{1}{2G_{xz}} & 0 \\ & & & 0 & 0 & \frac{1}{2G_{yz}} \\ \end{pmatrix} \begin{pmatrix} \sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \sigma_{xy}\\ \sigma_{xz}\\ \sigma_{yz} \end{pmatrix}
Formulas del Caso Tridimensional Ortotropo





Problema:



Para un resorte que cumple la ley de Hooke y que presenta como constante clásica de elasticidad el valor de 19.62 N/cm. Se le cuelga un objeto que causa una deformación de 58.86 cm. ¿Cuál es la masa del objeto?

K=19.62 N/cm             F=kx                  m=Kx/g
x=58.86                        W=mg         m=(19.62 N/cm)(58.86 cm)/9.81
g=9.81 m/s2                      Kx =mg             m/s2= 1154.83N/9.81 m/s2=
                                                                                                   117.72 Kg
m=117.72 Kg












Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)